
This article is the second part of a three-part series on machine learning. You can read Part 1 here.
The purpose of this article is to understand the details of logistic regression. What it is and how it’s used etc.
Let’s start with the definition. It is a classification algorithm for predicting values of a discrete variable. As one of the most popular and widely used classifications learning algorithm, it is also the foundation for the more advanced classification algorithms.
Here are some examples of where it can be applied: classifying emails as spam or not spam and identifying loan customers as potential defaulters. In these two cases, the variable y that we try to predict can take values {0,1} corresponding to negative and positive classes.
Linear regression:
Can we apply linear regression in this setup?
For example, let’s look at the following problem of predicting coronary disease based on the age. Obviously, the linear regression cannot be applied here due to the following reasons;
- The hypothesis will emit a continuous set of values, that can be in any range.
- Which doesn’t help directly predicting a discrete value?
- The value that we are trying to predict is {1=Y or 0=N}. But the values in the hypothesis may not necessarily match.
- By looking at the following plot it can be seen that the hypothesis results in values both less than zero and greater than one in some cases.
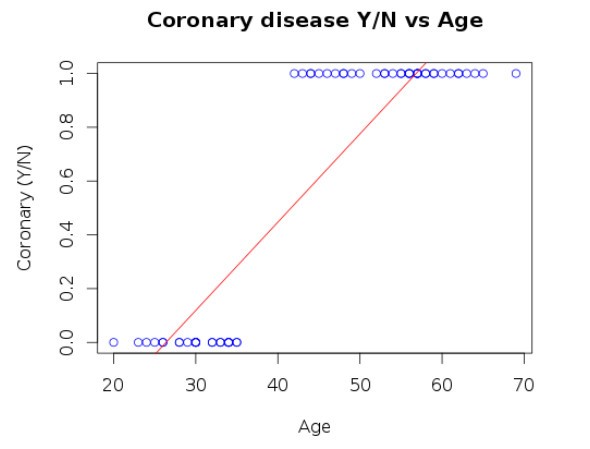
Supposing we do a reasonable approximation on top of this, we can use it to predict the discrete value.
- Let’s say we infer any value >0.5 as 1 and any values <0.5 as 0.
- As can be seen in the plot below, it is possible to classify/predict the coronary Y/N appropriately if we use this approach.
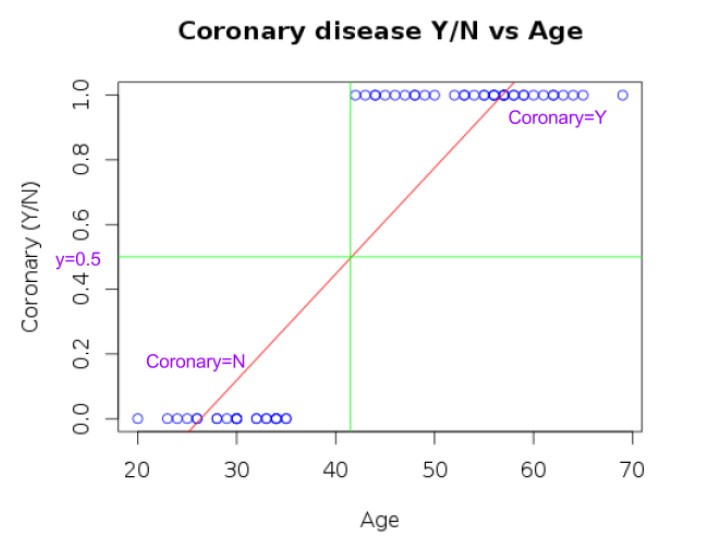
- But this may not work in all cases. For example, when we have a sufficient number of extreme/outliers points (with a higher age and coronary disease: Y) the regression line will change.
- This results in wrong predictions of the hypothesis.
- As seen above, actual predictions for some of the observations are <0 and >1 in some cases, even though the response variable is discrete with values 0 and 1.
Hence it is not a good idea to apply linear regression to classification problems. Though it may turn out to be a reasonable approximation in some cases.
Logistic regression:
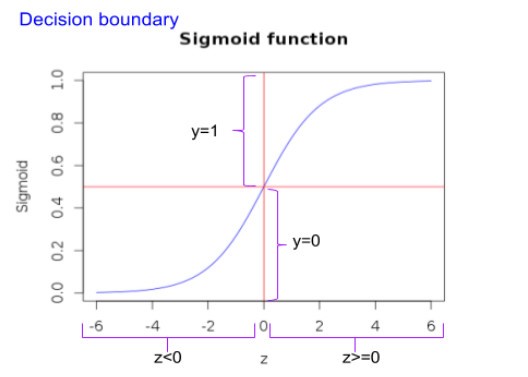
The first thing that we need to understand about logistic regression is that it has a hypothesis function that can emit values within the bounds of 0 and 1.

As can be seen below, the sigmoid function can constrain the values between 0 and 1. The curve starts with zero for negative values of z and slowly approaches 1. With a value of 0.5 for z=0 (i.e. ½ for z=0).
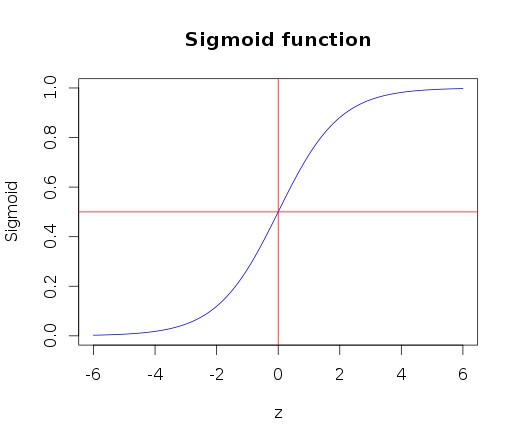
This function satisfies the requirement that the output of the hypothesis should be constrained between 0 and 1. With that, we should be able to fit the parameters theta (θ), with the data.
Before we look at the details of how the learning algorithm works, let’s look at the way to interpret the same.
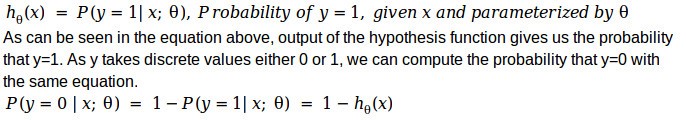
Decision boundary:
Let’s suppose we predict the values of y based on the following equation,
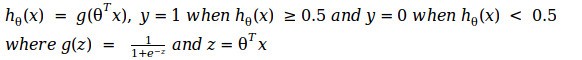
Now if we look back the plot of the sigmoid function, we can see that
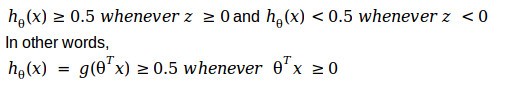
With this, let’s try to better understand, how the hypothesis makes its prediction.
As mentioned earlier, y=1 whenever z >= 0. Let’s take the case of the following data with two classes,
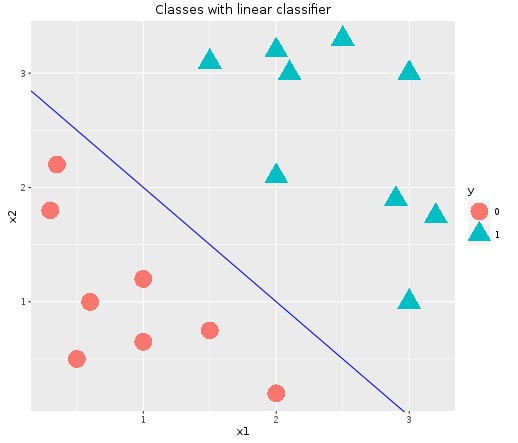
Let’s try to understand how the hypothesis function would turn out to be in this case,

The blue line that we are seeing in the plot is called the decision boundary. With this illustration, we can understand how to interpret the hypothesis function.
This example shows a linear classifier. There can also be non-linear classifiers as shown below in the plot.
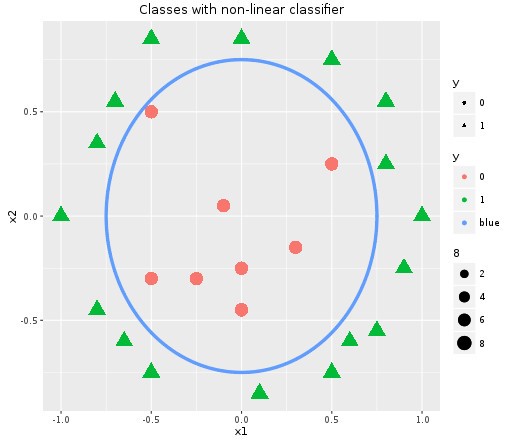
For this case let’s say we are bringing in non-linear parameters as well and the hypothesis function becomes as follows,
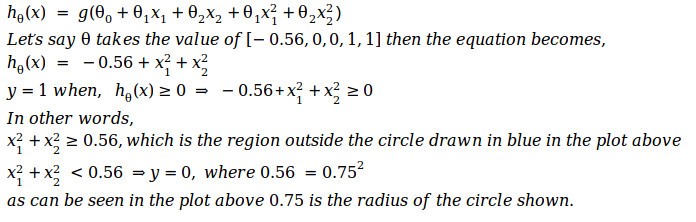
This decision boundary is a property of the hypothesis function and not of the data. Once we learn the parameters from the data, we can really throw away the data and start using the decision boundary to classify.
As a next step, we can now look at how the parameters fit in with the data, to come out with the hypothesis function.
Cost Function:
As we looked at in the case of linear regression, the first step in problem formulation of machine learning is to come out with the cost function and optimization objective.
Just to recap the problem setup,

As in the case of linear regression, we need to come out with a cost function. We can, in fact, try to use the same cost function
![]()
But unlike in the case of linear regression, it won’t be ideal to use it for logistic regression. Due to the non-linearity nature of the hypothesis function, this squared error cost function will not be a proper convex function in this case. With possibly multiple local optima points, it won’t be easier to optimize this cost function for logistic regression. Hence, we need to come out with an alternate cost function in this case.
The cost function that is used with logistic regression is,
![]()
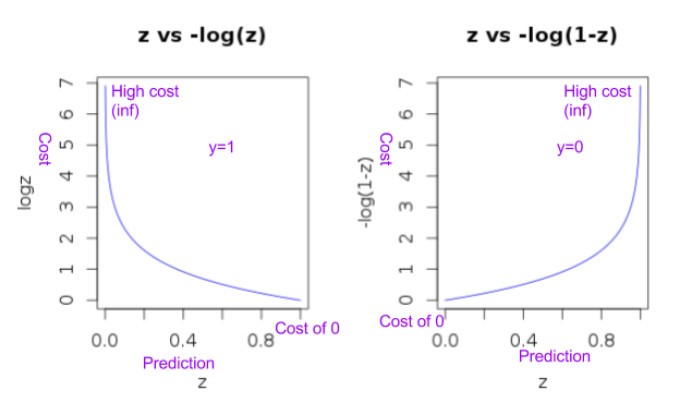
The intuition behind this function is as follows,
- When y=1 the function -log(h(x))
- Will penalize with really high value (i.e. infinity) when the prediction is 0 (as log (0) is -infinity and -log (0) is infinity).
- Whereas when prediction also becomes 1 the penalty resulting from this function will be 0 (as log (1) is 0).
- When y=0 the function -log(1-h(x))
- Will penalize with infinity when the prediction is 1 (as -log (1-1) is infinity).
- Whereas when the prediction also becomes 0 the penalty resulting from this function will be 0.
This intuition behind the cost function can be seen clearly from the plot below.
The plot also shows that this function will be a proper convex function.
The cost function we looked at above for the cases of y=0 and y=1 can be combined and written as follows,
![]()
It can easily be verified that this form results in the same cost function we looked at earlier. That is when y=1, the second term becomes 0, resulting in only -log(h(x)). And when y=0, the first term becomes 0 and resulting only -log(1-h(x)). Which is exactly what we looked at earlier.
Hence our cost function for logistic regression turns out to be,
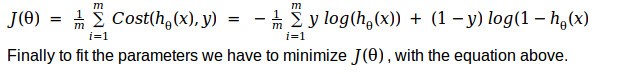
Although this function satisfies the constraints of a proper cost function (i.e. being convex) and correctness can be verified intuitively, this may not be the only function that can be used. But the actual reason for using this function relates to applying maximum likelihood estimation on top of the logistic regression problem setup. Details on the same and a nice derivation can be referred from this link.
Learning algorithm:
With the cost function and the problem setup that we looked at above, let’s try to understand how we apply gradient descent to solve the same to fit the parameters.
Generalized gradient descent algorithm as we looked at in the case of linear regression (Please refer to Part 1 for more details),

When we take the derivative of the cost function mentioned above the algorithm turns out to be,
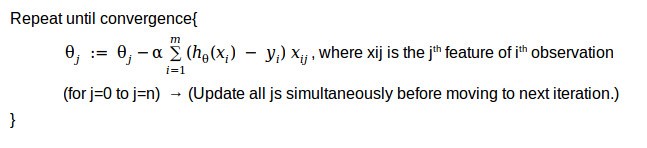
If you recollect this partial derivative term in the above algorithm looks identical to the one of linear regression. But the difference lies in the hypothesis functions.

We have gone through one of the most powerful and widely used classification algorithm in use. It also sets the foundation to understand other more complex machine learning algorithms like neural networks.
If you want to play around the code used for the illustration here, please refer to my git-hub link.
Reference 1
Reference 2



















